|
الألغاز اليابانية |
||
| لليابانيين دور كبير في اختراع وتطوير الكثير من الألغاز , واليابانيون بصورة عامة مولعون بألغاز الأرقام المنطقية ولهم الفضل في اختراع أو على الأقل تطوير أنواع من الألغاز التي سميت بأسماء يابانية وهذه الألغاز هي : سودوكو و كاكورو ( تقاطع المجموع )و والسلي لين (الحواجز) وهانجي و هاتوري . وقد سميت هذه الألغاز بالألغاز اليابانية على الرغم من أن قسما منها ليست اختراعا يابانيا لكنها طورت في اليابان وانتشرت على نطاق واسع وفي العديد من المجلات والكتب اليابانية . ونحن هنا ننشر هذه الألغاز مع نبذة تاريخية مبسطة عنها . وندعو كل من لديه فكرة ابتكار نوع جديد من الألغاز إلى مراسلتنا عسى أن نبتكر نوعا جديدا يسجل ابتكارا عربيا ونضع بصمتنا في التاريخ. | ||
|
سودوكو |
||
| لعبة سودوكو ( sudoku ) نشرت أول مرة في صحيفة أمريكية سنة 1979 ولكن الأمر أخذ شهرة واسعة في اليابان منذ عام 1986 وقد أصبح شائعا وعلى نطاق واسع منذ عام 2005. واللعبة في غاية البساطة حيث أنها عبارة عن 81 مربعا موزعا على تسعة مجاميع 3×3 المطلوب وضع الأرقام من 1 إلى 9 في هذه المربعات على أن لا يتكرر أي منها على نفس الصف أو العمود أو المجموعة.لاحظ الشكلين أدناه الذي يمثل اللغز على اليمين والحل على اليسار: | ||
|
|
|
|
| وظهرت هناك انواع عديدة من السودوكو وهي : | ||
| 1) السودوكو الصغير:بحجم(4×4) وبأربعة مجاميع , وبحجم ( 6×6) وبستة مجاميع كل مجموعة بأبعاد (2×3). | ||
| 2) السودوكو العملاق : بأبعاد (16×16) وبـ (16) مجموعة أو أكثر. | ||
| 3) السودوكو ذات المحورين: بإضافة شرط عدم تكرار أي رقم في المحورين. | ||
| 4) السودوكو الغير منتظم : نفس الشكل التقليدي باستثناء عدم انتظام المجاميع . | ||
| 5) السودوكو المتعدد : عبارة عن اتحاد أكثر من شبكة سودوكو في شبكة واحدة. | ||
| 6) السودوكو الفردي أو المتطابق : في هذا النوع يحدد عدد من المربعات بلون داكن ( رمادي عادة) والمطلوب أن يكون الأرقام في هذه المربعات فردية أو متطابقة حسب ما يطلبه اللغز. | ||
| 7) سودوكو الصورة: في هذا النوع يكون اللغز على شكل صورة معينة قبل الحل. | ||
| 8) السودوكو المختلط : يجمع بين نوعين أو أكثر من السودوكو. | ||
| 9) سودوكو المجموع (قاتل سودوكو) : عبارة عن شبكة سودوكو مقسمة إلى مجاميع كل منها تحمل مجموعا معينا والمطلوب ملئها بالأرقام ليكون مطابقا للمجموع المعطى ويكون سودوكو في نفس الوقت. | ||
|
كاكورو |
||
| كاكورو kakuro هو نوع من الألغاز يتكون من شبكة من المربعات بأبعاد مختلفة المطلوب ملئها بالأرقام من واحد إلى تسعة بحيث يكون مجموعها مطابقا للمجموع المعطى في نهاية كل صف أو عمود ويشترط عدم تكرار الأرقام التي يتم جمعها .لاحظ الشكلين أدناه الذي يمثل اللغز على اليمين والحل على اليسار: | ||
|
|
|
|
| وقد نشر هذا النوع من الألغاز لأول مرة سنة 1966 في إحدى مجلات ديل وهي مجلة أمريكية مختصة بالألغاز وهو نفس الناشر الذي نشر سودوكو لأول مرة.وسمي حينها بـ ( تقاطع المجموع ) . | ||
| وكما هو الحال بالنسبة لـ ( سودوكو ) فان جنون ككورو أخذ في الانتشار سريعا في اليابان عندما دخل إلى اليابان لأول مرة سنة 1980 من قبل ماكي كاجي ، رئيس ألغاز نيكولي وهو الذي أطلق عليه اسم (kasan kurosu) وهي الترجمة اليابانية لتقاطع المجموع ثم حوره إلى كاكورو (kakuro) سنة 1986 .ثم أصدر مجلدا حول ألغاز كاكورو وأتبعه باثنين وعشرين مجلدا لحد الآن وقد بيع من هذه المجلدات لحد الآن أكثر من مليون كتاب. | ||
| وحاليا فان ألغاز كاكورو من قبل نيكولي ينشر في أكثر من 100 مجلة وصحيفة يومية ويحتل المرتبة الثانية بعد سودوكو . | ||
|
الحواجز |
||
|
تسمى هذا النوع من الألغاز بأسماء عديدة منها الترابط الانزلاقي ( slitherlink ) والحواجز ( fences ) والسلي لين ( sli-lin ) وغيرها .يتكون هذا النوع من الألغاز من عدد من النقاط مرتبة على شكل مربعات بعض منها تحمل أرقاما ويشير كل عدد إلى عدد الحواجز التي يجب وضعها في كل مربع والمربعات التي لا تحمل أرقاما تعني ( أي عدد ) أي بالإمكان وضع أي عدد من الحواجز للمربعات التي لا تحمل أرقاما و المطلوب ربط النقاط الموجودة بحيث يكون عدد الحواجز عند كل مربع مطابقا للعدد المعطى ويشترط أن يكون الربط بين الحواجز على شكل منحني مغلق ولا يكون هنا أي حاجز مفصول لوحده .لاحظ الشكلين أدناه الذي يمثل اللغز على اليمين والحل على اليسار: |
||
|
|
|
|
| اخترعت ألغاز الحواجز في اليابان لأول مرة في 1989 ونشرت لأول مرة في العدد 26 من مجلة نيكولي بزل تايمز ( Nikoli's puzzle times ) لشهر حزيران من سنة 1989 . والتسمية الشائعة له في اليابان هي السلي لين ( sli-lin ) وبحلول عام 2006 بلغ ما صدر من قبل ألغاز نيكولي 17 كتابا يحوي كل منها على أكثر من تسعين لغزا . واليوم يحتل ألغاز الحواجر المرتبة الثالثة في اليابان بعد سودوكو وكاكورو. | ||
|
هانجي |
||
|
من أجمل الألغاز اليابانية بل من أجمل الألغاز على الاطلاق ألغاز هانجي أو ما اصطلحنا على تسميته (الصورة الرقمية ) . في هذا النوع من الألغاز نرى شبكة من المربعات الفارغة مرتبة على صفوف وأعمدة بأبعاد مختلفة . في بداية كل صف وعامود عدد أو مجموعة من الأعداد تمثل عدد المربعات المتجاورة في كل صف وعامود . وبعد حل الشبكة يظهر لنا صورة تدل على شيء معين. وقد طورت هذا النوع من الألغاز فأصبحت تمثل صورا بالألوان .معظم الألغاز تذكر لك اسم الصورة مسبقا . الشكل أدناه يمثل مثالا محلولا وهي صورة لباباي : |
||
|
|
||
|
تعود بدايات هذه اللعبة إلى سنة 1987 - على الرغم من وجود بعض الدلائل على تكوين الصور بالأرقام مع بداية القرن العشرين - ففي هذه السنة فاز الياباني نون ايشادا ( Non Ishida ) بمسابقة تصميم صورة باستعمال أضواء إحدى ناطحات السحاب المشتعلة والمنطفئة . ومن هنا ولدت فكرة تكوين الصورة بالأرقام . وفي سنة 1988 أصدر نون ايشادا ثلاثة ألغاز تحت اسم ( ألغاز فن النوافذ ) . وفي العام 1990 اخترع الإنكليزي جيمس دالجتي اسم ( نونوغرام ) على ألغاز فن تكوين الصور . وفي العام 1993 صدر أول كتاب للنونوغرام من قبل نون ايشادا في اليابان. وبعدها انتشرت ألغاز النونوغرام في السويد وجنوب أفريقيا والعديد من دول العالم, وصممت حديثا برامج كمبيوتر لتصميم وحل ألغاز النونوغرام. |
||
| وظهرت أنواع عديدة من ألغاز تكوين الصور وهي: | ||
| 1) التقليدي : وهو النوع التقليدي للغز حيث يعطي عدد المربعات المتصلة ببعضها في كل صف وعامود والمطلوب ايجاد الصورة. | ||
| 2) ربط المربعات : في هذا النوع يكون الأرقام والأعداد داخل الشبكة ويتم تكوين الصورة بربط الرقم أو العدد برقم أو عدد مماثل شريطة أن يكون الربط بعدد من المربعات مساوي للرقمين أو العددين المربوطين . | ||
| 3) كاسح الألغام : هذا النوع يشبه إلى حد كبير لعبة كاسح الألغام المتوفرة على برامج الويندوز , في هذا اللغز يكون الأرقام داخل الشبكة ويشير كل عدد إلى عدد النقاط الموجودة في المربع مع المربعات المحيطة الثمانية المحيطة بها . وينتج بعد حلة الصورة المطلوبة. | ||
| 4) المتاهة : هذا اللغز عبارة عن متاهة وقد وضعت عدد من النقاط الملونة داخله والمطلوب ربط كل نقطتين بلون معين من خلال العبور بالمتاهة ليتكون الصورة بعد ذلك. | ||
| 5) ربط النقاط: في هذا النوع يكون لدينا عدد من النقاط المرقمة والمطلوب ربطها بشكل متسلسل , هذا النوع لا يحتاج إلى تفكير كثير وهي مناسبة جدا للأطفال. | ||
|
الصبغ المتتابع |
||
|
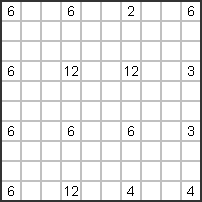
شبيهه بالهانجي مقسمة إلى غرف ومربعات حيث يدل كل رقم على عدد المربعات السوداء (يجب صبغ جميع مربعات الغرفة الواحدة) .لاحظ المثال ادناه: |
||
|
|
|
|
|
الزجاجة المكسورة |
||
|
المطلوب إيجاد المناطق السوداء حيث يشير الدوائر السوداء إلى وجود مناطق سوداء حوله أكثر من المنطق البيضاء.وتشير الدوائر البيضاء إلى وجود مناطق بيضاء حوله أكثر من السوداء. والدوائر الرمادية تدل على عدد متساوي من المناطق البيضاء والسوداء حوله. لاحظ المثال أدناه: |
||
|
|
|
|
|
هياواكي |
||
|
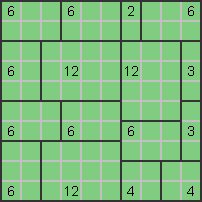
المطلوب في هذا النوع من الألغاز وضع حواجز (مربعات سوداء) ضمن قواعد معينة. تنقسم الشبكة إلى غرف تحتوي كل غرفة على عدد من المربعات الفارغة. الغرف التي تحمل أرقاما يجب أن تحوي عددا مساويا من الحواجز ,أما التي لا تحمل أرقاما فمن الممكن أن يكون أي عدد من الحواجز. كما يجب أ لا تتجاور حاجزان (أفقيا أو عموديا) ويجب أن لا تتجاور مربعات بيضاء لثلاثة غرف متجاورة (كما في الشكل على اليمين) ويجب أ لا يكون المربعات البيضاء منفصلة (الشكل على اليسار). |
||
|
|
|
|
| لاحظ المثال أدناه الذي يمثل اللغز على اليمين والحل على اليسار. | ||
|
|
|
|
|
هيتوري |
||
|
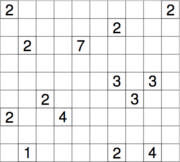
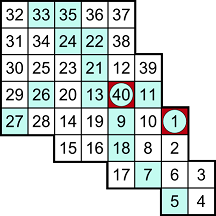
الهيتوري هي شبكة مكونة من مجموعة من المربعات ذات أرقام وأعداد .والمطلوب حذف مجموعة من الأرقام والأعداد بحيث تكون الأرقام الباقية متصلة مع بعضها البعض ولا يتكرر أي منها على نفس العمود أو الصف . لاحظ الشكلين أدناه الذي يمثل اللغز على اليمين والحل على اليسار: |
||
|
|
|
|
|
لا يعرف الكثير عن ألغاز الهيتوري . اخترعت ألغاز الهيتوري من قبل ألغاز نيكولي بعد فترة وجيزة من اختراع سودوكو وكاكورو واستنادا إلى الموسوعة الحرة ( ويكيبديا ) فان أول ظهور للهيتوري كان في شهر آذار من سنة 1990 وفي العدد 29 من مجلة ألغاز نيكولي . ومنذ ذلك الحين تظهر ألغاز الهيتوري بصورة منتظمة في مجلة ( نيكولي بزل تايمز ) وهي تعني باليابانية ( اتركني وحيدا ) . |
||
|
سفن المعركة |
||
|
هذا النوع من الألغاز لا يمكننا اعتباره لغزا يابانيا وإنما أودرناها هنا لكونها شبيهة بالألغاز اليابانية . وكان هذا اللغز لعبة تلعب من قبل لاعبين ولم تأخذ شكل لغز يحل من قبل شخص واحد الا في عام 1982 حيث نشرت لأول مرة في مجلة ( Humor and Juegos ) الأرجنتينية وباللغة الاسبانية وفي عددها الصادر في شهر تشرين الثاني من ذلك العام . وشكلها التقليدي عبارة عن شبكة بأبعاد ( 10×10 ) وقد أخفيت فيها عشرة سفن وهي ( سفينة حربية واحدة بطول أربعة مربعات, وطرادان -سفينة المطاردة- بطول ثلاثة مربعات , و ثلاثة مدمرات بطول مربعين , وأربعة غواصات بطول مربع واحد ) . أما المعطيات فهي عدد قطع السفينة في كل صف وعمود مع بعض قطع السفينة داخل الشبكة . لاحظ الشكلين أدناه الذي يمثل اللغز على اليمين والحل على اليسار: |
||
|
|
|
|
|
كوروماسو |
||
|
المطلوب في هذا اللغز وضع حواجز (مربعات سوداء) بحيث يكون عدد المربعات المحيطة بالمربعات التي تحمل الأرقام (أفقيا وعموديا) مساويا للرقم الذي يحمله .وتعتبر المربعات التي تحمل الأرقام مربعا فارغا ولا يجوز وضع الحواجز على مربع يحمل رقما ولا يجوز أن تتجاور حاجزان أفقيا وعموديا ويجب أن يكون بقية المربعات الفارغة (البيضاء) متصلة فيما بينها. لاحظ المثال أدناه: |
||
|
|
|
|
| ولن نورد ألغازا من هذا النوع في هذا الموقع لوجود لعبة خاصة به. | ||
|
نوريكاب |
||
| النوريكاب أو ( الجزر والبحار ) نوع من الألغاز المطلوب فيها فصل المناطق المشار إليها بأرقام بعضها عن بعض بمربعات سوداء على أن يحمل كل منطقة عددا من المربعات مساويا له ولا يتشكل هنالك أية مربعات سوداء بأبعاد (2×2) .لاحظ الشكلين أدناه الذي يمثل اللغز على اليمين والحل على اليسار: | ||
|
|
|
|
| ولن نورد ألغازا من هذا النوع في هذا الموقع لوجود لعبة خاصة به. | ||
|
سيكاكو |
||
| المطلوب في هذا النوع من الألغاز تقسيم الشبكة إلى مناطق مستطيلة أو مربعة بعدد من المربعات مساوية لكل رقم .لاحظ الشكلين أدناه الذي يمثل اللغز على اليمين والحل على اليسار: | ||
|
|
|
|
| ولن نورد ألغازا من هذا النوع في هذا الموقع لوجود لعبة خاصة به. | ||
|
ستريمكو |
||
| هذا نوع حديث من الألغاز والمطلوب فيها هو اكمال المربعات (أو الدوائر ) الفارغة بالأعداد على أن لا يتكرر أي عدد افقيا أو عموديا أو ضمن المجموعة الواحدة . وأدناه ثلاثة ألغاز مع الحل وللاطلاع على المزيد من الألغاز ندعوكم لزيارة الموقع www.strimko.com | ||
|
|
|
|
|
|
|
|
|
|
|
|
|
ترايكون |
||
|
الترايكون نوع من الألغاز المنطقية الحديثة العهد . يتألف لغز الترايكون من شكل هندسي متكون من المثلثات فقط وفي داخل كل مثلث مجموع الأرقام المحيطة به. والمطلوب إيجاد الأرقام المحيطة بكل مثلث .أضلاع المثلث الحرة ( الغير المشتركة مع مثلث آخر) يجب أن يحملا نفس الرقم . وبجانب كل لغز لوحة متكونة من جميع الاحتمالات الممكنة حيث لا يجوز تكرار أي احتمال . لاحظ الأمثلة أدناه - على اليسار - والحل - على اليمين-.ويتخذ الترايكون أحجاما عديدة ويشار لها بأكبر احتمال موجود فيه ( 333 , 444 , 555 , 666 ) وكلما كان كبيرا كلما ازدادت صعوبة اللغز . وينشر شهريا مجموعة من الألغاز ( غالبا 8 ألغاز ) يعطي كل منها حرفا واحدا بعد حل اللغز ليتشكل منها كلمة السر ويمنح صاحب الحل الصحيح كتاب الكتروني مجاني . وللاستمتاع بحل المزيد من ألغاز الترايكون قم بزيارة الموقع www.trigonpuzzles.com . |
||
|
|
||
|
|
||
|
|
||
|
|
||
|
المسار الأبجدي |
||
|
من الألغاز الحديثة العهد لغز المسار الأبجدي. في هذا النوع من الألغاز عليك إيجاد جميع الأحرف الأبجدية المخفية الـ (25) بدأ من الحرف (A) وانتهاء بالحرف (Y) حيث يجب أن يتصل كل حرف بالحرف الذي يليه أفقيا أو عموديا أو قطريا ,كما يجب أن يقع كل الحرف ضمن الصف أو العمود أو القطر المشار اليه .لاحظ المثال أدناه الذي يمثل اللغز على اليمين والحل على اليسار. |
||
|
|
|
|
|
للاطلاع ولعب ألغاز (المسار الأبجدي والجسور والفليمينو والفوتوشيكي والكاكوراسو والمصابيح والمخيمات) قم بزيارة الموقع www.brainbashers.com |
||
|
الجسور |
||
|
المطلوب في هذا النوع من الألغاز ربط الجزر بجسور بحيث يكون لكل جزيرة عدد محدد من الجسور , لا يجوز الربط لأكثر من جسرين كما لا يجوز وضع أي جسر فوق الآخر. لاحظ المثال على اليمين والحل على اليسار: |
||
|
|
|
|
|
فليمينو |
||
| يشبه هذا النوع من الالغاز بالنوريكاب الا أنه بدون حواجز . لاحظ اللغز على اليمين والحل على اليسار: | ||
|
|
|
|
|
فوتوشيكي |
||
| المطلوب ملىء المربعات الفارغة بالأرقام على أن لا يتكرر نفس الرقم في نفس الصف أو العمود (يجوز تكرار الرقم قطريا) ,كما يجب مراعاة أن الرقم باتجاه علامة الأكبر (>) أكبر من الرقم الذي يجاوره. لاحظ المثال والحل: | ||
|
|
|
|
|
كاكوراسو |
||
|
ا المطلوب التأشير على المربعات الفارغة (اختيار المربعات الفارغة) بحيث يكون الناتج مساويا للمجموع المعطى (يمين وأسفل) حيث أن قيمة مربعات الصف الأول هي واحد والصف الثاني اثنان والثالث ثلاثة والرابع أربعة ,في حالة الجمع العمودي. أما في حالة الجمع الأفقي فإن قيمة مربعة العمود الأول تساوي واحد والثاني اثنان والثالث ثلاثة والرابع أربعة . لاحظ المثال المحلول ادناه: |
||
|
|
|
|
|
المصابيح |
||
| المطلوب إضاءة جميع مربعات الشبكة حيث يضيء كل مصباح جميع المربعات حوله (أفقيا وعموديا) وليس قطريا . تشير الأرقام إلى عدد المصابيح حول المربع (أفقيا وعموديا فقط) ولا يجوز أن يضيء أي مصباح مصباحا آخر. لاحظ المثال أدناه: | ||
|
|
|
|
|
ناطحات السحاب |
||
|
في هذا اللغز المطلوب ملئ المربعات الفارغة بالأرقام ,حيث يشير كل رقم إلى عدد طوابق العمارة أو ناطحة السحاب. ويشير الأرقام حوله إلى عدد العمارات الممكن رؤيتها فإذا كانت العمارة ذات الطوابق الأربعة في المقدمة فسيحجب عنا روية بقية العمارات والعكس صحيح فإذا كانت العمارة الأصغر ذات الطابق الواحد قي المقدمة ويليه الثاني ثم الثالث ثم الرابع فسيكون من الممكن رؤية العمارات الأربعة جميعا .يجب مراعاة عدم تكرار نفس الرقم أفقيا وعموديا. لاحظ المثال أدناه: |
||
|
|
|
|
|
المخيمات |
||
|
المطلوب كشف أماكن المخيمات حيث يرتبط كل خيمة بشجرة واحدة فقط وتشير الأرقام أعلى ويسار اللغز إلى عدد المخيمات .لا يرتبط أي خيمة بشكل قطري بأية شجرة (تقع أفقيا وعموديا مباشرة وبدون فاصل) ولا يتجاور أية خيمة مع أية خيمة أخرى (أفقيا وعموديا وقطريا) . لاحظ المثال أدناه: |
||
|
|
|
|
|
لتس |
||
|
يتكون شبكة اللتس من غرف مختلفة الأشكال والأحجام والمطلوب ملئها بالأشكال الرباعية (تترامينو) بحيث يشكل شكلا متصلا غير مفصول. لا يجوز أن تلتقي الأشكال المتشابه أفقيا أو عموديا كما لا يجوز أ تتشكل أي مربع (2×2). لاحظ اللغز على اليمين والحل على اليسار: |
||
|
|
|
|
|
ماسيو |
||
|
شبيه للحواجز. المطلوب رسم خط متصل يشكل منحني مغلق . كما هي الحال في الحواجز لا يجوز أي يتقاطع أي خط ولا يجوز أن يشكل منحنيان منفصلان ويكون الانتقال أفقيا وعموديا فقط. ويخضع هذا النوع من الألغاز لبعض القواعد وهي أن يكون الخط المار من الدوائر البيضاء مستقيما ويجب أن ينحني الخط المار من الدائرة البيضاء من طرف واحد على الأقل . بينما يكون الخط المار من الدائرة السوداء مائلا (غير مستقيم) ويجب أن يمتد لمربعين على الأقل. كما يجب المرور من جميع الدوائر بدون استثناء. لاحظ المثال المحلول أدناه: |
||
|
|
|
|
|
ياجيلين |
||
|
شبيه للحواجز. المطلوب رسم خط متصل يشكل منحني مغلق . كما هي الحال في الحواجز لا يجوز أي يتقاطع أي خط ولا يجوز أن يشكل منحنيان منفصلان ويكون الانتقال أفقيا وعموديا فقط يتم وضع حواجز (تلوين المربعات باللون الأسود) في حالة عدم المرور بها . تشير الأرقام إلى عدد الحواجز (المربعات السوداء) في اتجاه كل سهم. لا يجوز تجاور أي مربعين كما لا يجوز المرور او وضع الحواجز على المربعات التي تحمل أرقاما. لاحظ المثال أدناه: |
||
|
|
|
|
|
سورارومو |
||
|
شبيه للحواجز. المطلوب رسم خط متصل يشكل منحني مغلق . كما هي الحال في الحواجز لا يجوز أي يتقاطع أي خط ولا يجوز أن يشكل منحنيان منفصلان ويكون الانتقال أفقيا وعموديا فقط الخطوط المتقطعة تشير إلى البوابات ويجب المرور من جميع البوابات. يتم البدء من المربع المفتوح (الرقم خمسة في هذا المثال) ويشير الرقم داخله إلى عدد البوابات التي سيمر بها خلال مساره بينما تشير الارقام (داخل المربعات السوداء إلى تسلسل مرور الخط المنحني ( اذا افترضنا بأننا بدأنا بالرقم خمسة نزولا ثم انتقلنا باتجاه عقارب الساعة فسنمر من البوابة الأولى أسفل اليمين ثم المجاور للرقم 2 ثم أعلى اليمين ثم المجاور للرقم 4 وهكذا) . لاحظ المثال أدناه: |
||
|
|
|
|
|
طريق الدولة |
||
|
ان (طريق الدولة) هي الترجمة الحرفية للتسمية الانكليزية (country road) . يتألف من شبكة مقسمة إلى غرف يحتوي بعضها على أرقام يدل كل رقم على عدد المربعات التي يجب المرور بها لتشكيل منحني مغلق . الغرف التي لا تحمل أرقاما تعني (أي عدد من المربعات) . لاحظ المثال أدناه: |
||
|
|
|
|
|
الحقيبة |
||
|
هذا النوع من الألغاز يجمع بين ألغاز الحواجز وألغاز الكوروماسو . المطلوب رسم منحني مغلق ويشير الأرقام إلى عدد المربعات التي الأفقية والعمودية داخل الحقيبة ,لاحظ المثال ادناه: |
||
|
|
|
|
|
حزم الأشعة |
||
|
المطلوب ربط جميع الدائر بعضها ببعض يجب أن ينطلق الشعاع (الخط) من جهة النقطة دائما ويشير الأرقام إلى عدد المرات التي يغير فيها الشعاع اتجاهه ليلتقي بالنقطة الأخرى ز لاحظ المثال أدناه: |
||
|
|
|
|
|
التقسيم |
||
| المطلوب تقسيم المنطقة غلى عدة مناطق تحمل كل منها نفس الأحرف .لاحظ المثال ادناه: | ||
|
|
|
|
|
ياجيسان |
||
|
المطلوب كشف أماكن ويشير الحواجز (المربعات السوداء) حيث يشير الأسهم والأرقام إلى عدد الحواجز (المربعات السوداء) في اتجاه كل سهم. لاحظ المثال أدناه: |
||
|
|
|
|
|
ربط الأرقام |
||
| هذا النوع من الألغاز ذات قواعد بسيطة والمطلوب ربط أزواج الارقام بخطوط (أفقيا وعموديا فقط) دون تقاطع الخطوط ودون المرور من مربع فيه رقم آخر. لاحظ المثال أدناه: | ||
|
|
|
|
|
التموجات |
||
|
شبيه بالسودوكو الغير منتظم مع بعض الاختلافات البسيطة. المطلوب ملئ الغرف بالأرقام (حسب عدد المربعات في كل غرفة) بدون تكرار في الغرفة الواحدة وإذا صادف تواجد رقمين في نفس الصف أو العمود فيجب أي يكون بينها وبين الرقم الآخر مسافة مساوية أو أكثر منه (من الرقم). لاحظ المثال أدناه: |
||
|
|
|
|
|
جوكيجين |
||
|
الجوكيجين عبارة عن شبكة من المربعات يتخللها دوائر ذات أرقام . يمثل هذه الأرقام عدد الخطوط المارة خلاله .وبخلاف معظم الألغاز اليابانية تشترط الجوكوجين أن لا يتشكل أي منحني مغلق وبأي حجم كان . لاحظ المثال أدناه. |
||
|
|
|
|
|
جويشي |
||
|
هذا النوع من الألغاز عبارة عن رفع القطع بطريقة معينة. المطلوب البدء من قطعة معينة ثم الانتقال أفقيا وعموديا (لا يجوز الرجوع) ولا يجوز الانتقال إلى مربع فارغ لحين رفع جميع القطع . لاحظ المثال أدناه الذي يمثل اللغز على اليمين والحل (الأرقام تشير إلى تسلسل رفع القطع): |
||
|
|
|
|
|
كين كون كان ( المرايا ) |
||
|
الأصح تسمية هذا النوع من الألغاز بـ (المرايا العاكسة) يتألف هذا النوع من عدة غرف والمطلوب وضع مرآة عاكسة واحدة فقط في كل غرفة بوضع مائل يسمح بعكس الشعاع المنبعث من حرف إلى نفس الحرف المقابل (جميع المرايا عاكسة في الوجهين) .يشير الرقم المجاور للحرف إلى عدد مرات الانعكاس ليصل إلى الحرف المناظر له. لا يجوز مطلقا انطلاق الشعاع إلى حرف آخر. لاحظ المثال أدناه: |
||
|
|
|
|
|
هيتادو |
||
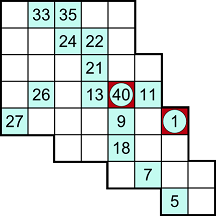
| هذا النوع من الألغاز ذات قواعد بسيطة جدا. المطلوب الانتقال من الرقم (واحد) افقيا وعموديا وقطريا حتي آخر رقم (40) في هذا المثال. | ||
|
|
|
|
|
مجموع الخط |
||
|
في هذه النوع من الألغاز المطلوب ملئ الشبكة بالأرقام المعطاة أفقيا وعموديا يحيث يتم تجزئة كل عدد إلى عددين أو أكثر يكون في مجموعها مساويا للعدد المعطى. فمثلا في الصف الأول يكون مجموع (9+1678) مساويا غلى الرقم المعطى 1687 وهكذا بالنسبة لبقية الأعداد الأفقية والعمودية . مع مراعاة عدم تكرار أي رقم أفقيا وعموديا. لاحظ المثال ادناه. |
||
|
|
|
|
|
تقاطع الأرقام |
||
|
المطلوب ملئ الشبكة بالأرقام المعطاة أفقيا وعموديا وقد يتم تحديد الفواصل (المربعات السوداء) أو لا يتم ذلك لزيادة صعوبة اللغز كما هو الحال في المثال أدناه: |
||
|
|
|
|
|
كاروجي |
||
|
من الألغاز التي يعود إلى اليابانيين الفضل في ابتكارها ألغاز (كاروجي) . يتكون هذا النوع من الألغاز من شبكة فارغة من المربعات بأبعاد (3×3) و (4×4) و (5×5) ومجموعة من التعليمات على يسار الشبكة . المطلوب وضع الأحرف على الشبكة ضمن القواعد الخاصة على يسار الشبكة. تتضمن القواعد : الأحرف في كل سطر وكلها معطى. والمجموعة الثانية هي التي تدل على مواقع الأحرف في الأعمدة (مثلا X=G تعني بأن X في نفس عمود G ) وغيرها كما هو موضح في المثال أدناه: |
||
|
|
|
|
|
إطفاء المصابيح (Lights Out) |
||
|
هذا النوع من الألغاز يتألف من شبكة من المربعات (بأبعاد 5×5) كل مربع يمثل مصباحا وزرا للإطفاء في نفس الوقت ,يمثل كل مربع أسود مصباحا مضاء وكل مربع أبيض يمثل مصباحا مطفأ. عند الضغط على كل زر (مصباح) فإن جميع المصابيح المحيطة به والمطفأة (أفقيا وعموديا) تضاء والمضاءة تطفئ. والمطلوب إطفاء جميع المصابيح. الصورة الأولى توضح المصابيح التي ستطفأ وهي (ثلاثة عند الضغط على مصباح الزاوية وأربعة عند مصابيح الجوانب وخمسة عند أي مصباح من المصابيح الداخلية التسعة). الصورة الثانية على اليسار تمثل اللغز. طريقة حل هذا النوع من الألغاز سهلة للغاية فما عليك سوى الضغط تحت كل مصباح مضاء بدأ من الصف الثاني حتى الخامس وبذلك يتم إطفاء جميع المصابيح عدا الصف السفلي (تسمى هذه العملية بعملية الثلم) ثم (الخطوة الثانية) الضغط على المصباحين الأول والثاني (على اليمين) إذا كان المصباح الأول من اليسار في الصف السفلي مضاء، والضغط على المصباحين الأول والرابع (من اليمين) إذا كان المصباح الثاني من اليسار في الصف السفلي مضاء، والضغط على المصباح الثاني فقط في الصف الأول (من اليمين) عدا كان المصباح الثالث (في المنتصف) في الصف السفلي مضاء. ثم البدء بعملية (الثلم) مرة أخرى وستحل بسهولة. هذه الطريقة هي طريقة سهلة لكنها ليست الطريقة المثلى للحل. وقد تفرعت من هذا النوع من الألغاز تفريعات كثيرة بأبعاد مختلفة وألوان متعددة وطرق إطفاء مختلفة ولكل منها طرق حل مختلفة. وللإطلاع على هذه الألغاز انتقل إلى هذا الموقع. اضغط هنا |
||
|
|
|
|
| توضيح لعمل المصابيح | اللغز | |
|
|
|
|
| اللغز بعد عملية الثلم | اللغز بعد الثلم والضغط على المصابيح (الأول والثاني - والأول والرابع - والثاني) | |
|
الغير ميت (Undead) |
||
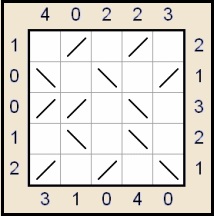
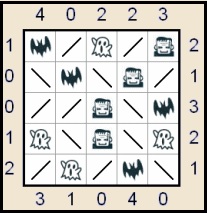
| يتكون هذا النوع من الألغاز من شبكة مختلفة الأبعاد بعضها فارغة وبعضها ذات مرايا (بوجهين عاكسين) المطلوب وضع ثلاثة أنواع من الكائنات في المربعات الفارغة بحيث يحقق العدد المرئي المطلوب. الأشباح لا ترى مباشرة لكنها ترى بالمرآة العاكسة والخفاش على العكس ترى مباشرة لكنها لا ترى بالمرآة العاكسة وزومبي (الأحياء الأموات أو المومياء) يرى مباشرة وبالمرآة العاكسة ايضا. ويعطى عدد كل كائن مسبقا في بعض الألغاز. الشكل ادناه يمثل اللغز وحله على اليسار. | ||
|
|
|
|
|
سكة الحديد (Track) |
||
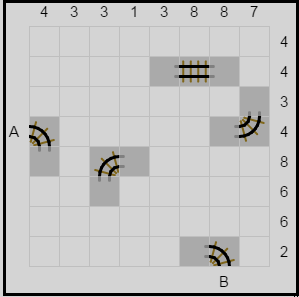
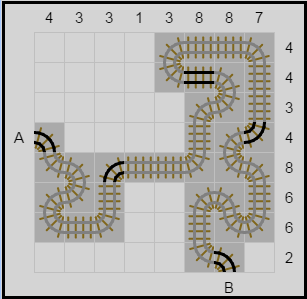
| اصطلحنا كلمة (سكة الحديد) بدل من الكلمة الأصلية (طريق) على هذا النوع من الألغاز وذلك لتجنب الالتباس مع الغاز أخرى تحمل أسماء مرادفة. المطلوب في هذا النوع من الألغاز إيجاد طريق سكة الحديد وفقا للمعطيات حيث يدل كل رقم على عدد قطع السكة افقيا وعموديا. للاحظ اللغز وحله على اليسار. هذا النوع من الألغاز تجده في الموقع إضغط هنا. | ||
|
|
|
|
|
ألغاز المغناطيس (Magnets) |
||
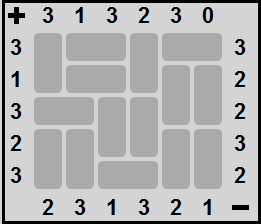
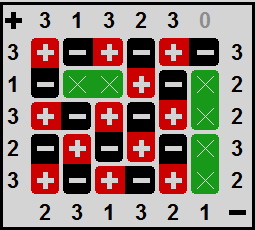
| تتألف ألغاز المغناطيس من شبكة مختلفة الأحجام والمطلوب إيجاد عدد ووضعية المغانط وفق المعطيات حيث يدل كل عدد اعلى ويسار اللغز على عدد الأقطاب الموجبة بينما يدل الأعداد يمين وأسفل الشبكة على عدد الشحنات السالبة. طبعا لا يجوز وضع أقطاب متشابه متجاورة حيث أنها ستتنافر. لاحظ اللغز وحله على اليسار. ولمزيد من الاطلاع اضغط هنا. | ||
|
|
|
|
|
الخريطة (The map) |
||
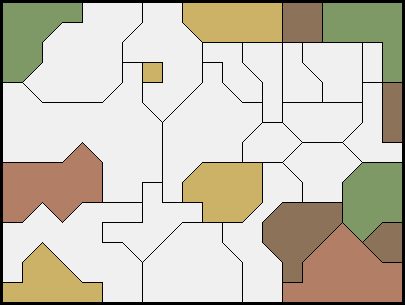
| ألغاز الخرائط تستند إلى نظرية رياضية تقول (بالإمكان صبغ أية خريطة بأربعة ألوان دون أن يتجاور أية منطقتان -دولتان مثلا- بنفس اللون). المطلوب صبغ جميع مناطق الخريطة بأربعة ألوان دون أن يشترك أية منطقتين بنفس اللون. الصعوبة هي في أن بعض المناطق مصبوغة مسبقا. لاحظ اللغز حله على اليسار. | ||
|
|
|
|